Topic C9 — Hypothesis Testing

Table of contents

Topic C9 — Hypothesis Testing

Null hypothesis and alternative hypothesis

Null hypothesis, $H_0$: presumed default state of nature or status quo. In specifying $H_0$, always contains an equality, i.e. $H_0 =$ or $H_0 \leq$ or $H_0 \geq$.
Alternative hypothesis, $H_A$: a contradiction of the default state of nature or status quo. Usually, $H_A$ is the outcome we want to test, the “desired” outcome.

We use sample information to infere unknown population parameters. We do hypothesis testing: we determine whether the evidence from the sample contradicts $H_0$.

Outcomes:

Reject $H_0$: sample evidence inconsistent with $H_0$
Do not reject $H_0$: evidence not inconsistent with $H_0$

Importantly, we can never accept $H_0$.

Two-tails: $H_0: \mu = \mu_0$vs $H_A: \mu \neq \mu_0$. If we use $\neq$, we say that both tails matter in order to assess $H_0$. Interpretation of the test: “Has no impact”.
One-tail: $H_0: \mu \leq \mu_0$vs $H_A: \mu > \mu_0$. Interpretation of the test: “Does not increase”. Look at the sign of $H_A$ to assess which tail to use.

Porcedure

Identify the relevant population parameter of interest.
Determine whether it is a one or a two-tailed test.
Include some form of the equality sign in $H_0$ and use $H_A$ to establish a claim.

Hypothesis test using CIs

Decision rule

Reject $H_0$ if the CI does not contain the value of $H_0=\mu_0$
Do not reject $H_0$ if CI does contain the value of $H_0 = \mu_0$

Hypothesis test using the p-value

Assume $H_0$ is true and see if sample evidence contradicts it.

The p-value is the likelihood of obtaining a sample statistic at least as extreme as the one in the sample, under the assumption that $H_0$ is true.

If the null hypothesis is true, how likely is that I have a sample at least as extreme as the one I have?

Caluclate the test statistic of your sample.
Check what is the area associatied with this $z$
Check if the are is greater (or smaller, depending on the specification of your test) than the area associated with the significance level you choose.

The p-value tells you the probability that this sample result would be generated if $H_0$ was true. Small p-value = small probability the null is true

Hypothesis test using the critical value

Reject the null hypothesis if the z-score is greater than some critical value.

Standardize the sample mean using the sample formula. This is your test statistic.
Check if it’s greater (or smaller, depending on the type of test) than the $z_{\alpha/2}$ with significance level $\alpha$.

Test statistics for the poplation mean

Same “brick” of formula that you used to compute CI.

Not in the formula sheet! $ \frac{\bar{x}-\mu_0}{\sigma/\sqrt{n}} $ or $ \frac{\bar{x}-\mu_0}{s/\sqrt{n-1}} $ if $\sigma$ unknown.

Test statistics for the population proportion

Not in the formula sheet! $ \frac{\bar{p}-p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}} $

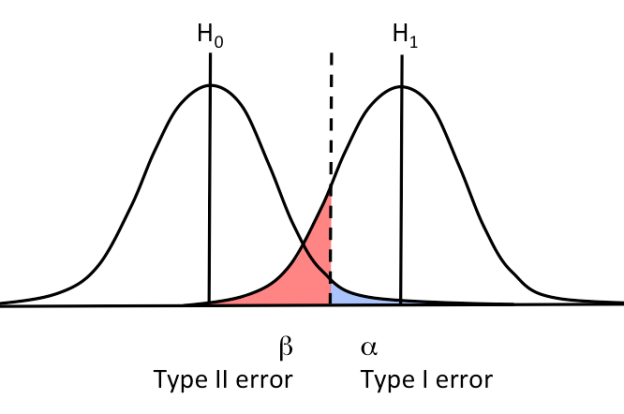
Type I and Type II errors

Type I: $H_0$ is true but we believe in $H_A$ (i.e. we don’t believe in $H_0$).
Type II: $H_0$ is not true but we believe in $H_0$ (i.e. we don’t believe in $H_A$).
Type I: we reject $H_0$ when $H_0$ is true.
Type II: we fail to reject $H_0$ when $H_0$ is false.
Type I: measured by $\alpha$, significance level
Type II: measured by $\beta$, power of the test.

Both depend of the standard error.

	$H_0$ true	$H_0$ not true
Reject $H_0$	Type I error False positive $\alpha$	Correct decision Power $1-\beta$
Do not reject $H_0$	Correct decision Confidence $1-\alpha$	Type II error False negative $\beta$

A decrease in $\alpha$ will increase $\beta$.

If the null hypothesis is “not pregnant”, the following show type I and II error.

error_types

error_types2